ストークスの式

こんにちは、ヘルメット犬(@helmet_dog)です。

この記事では

• ストークスの式とは
• ストークスの式の導出

について整理します!

ストークスの式とは

ストークスの式とは

粒子が流体中を沈降するときに最終的に到達する速度を表す式

になります。

例えば、スカイダイビングすると、最初は加速しながら落下しますが、最終的には一定速度になります。

これが流体中の粒子でも起きているわけですね。最終的に到達する速度を終末沈降速度と言います。

終末沈降速度を表す式には代表的なものとして3つあります。

レイノルズ数(Re)			式の名称		式
Re≦1			ストークスの式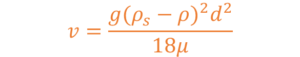
1<Re≦500			アレンの式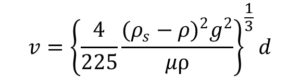
500<Re≦105			ニュートンの式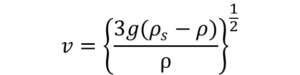

＜各記号の意味＞

v	粒子の沈降速度(cm/s)	g	重力加速度(cm/s2)
ρs、ρ	粒子及び水の密度(g/cm3)	d	粒子の直径(cm)
μ	水の粘度(g/cm/s)	Re(レイノルズ数)	dvρ/μ

3つの式はレイノルズ数(Re)に応じて使い分けられます。
Reは流体における慣性力と粘性力の比を表す次元のない数字(無次元数)です。
簡単に言えば、値が大きいほど流体の流れが乱れていることを表します。

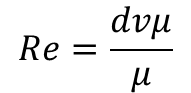
表に従えば、Reが1以下の小さい領域、すなわち流れの乱れがすくない領域でストークスの式が使えるわけですね!

実際、排水処理の沈殿池(粒子を沈殿させる池のような設備)で取り扱う粒子は直径d、沈降速度vが小さい、すなわちReが小さく、ほとんどストークスの式に従います。

よって、ストークスの式が最も重要で、試験にも出題されやすい内容になります。

ストークスの式の導出

では、ストークスの式はどのように導かれるのでしょうか。

流体中を沈降する球体上の粒子を考えます。

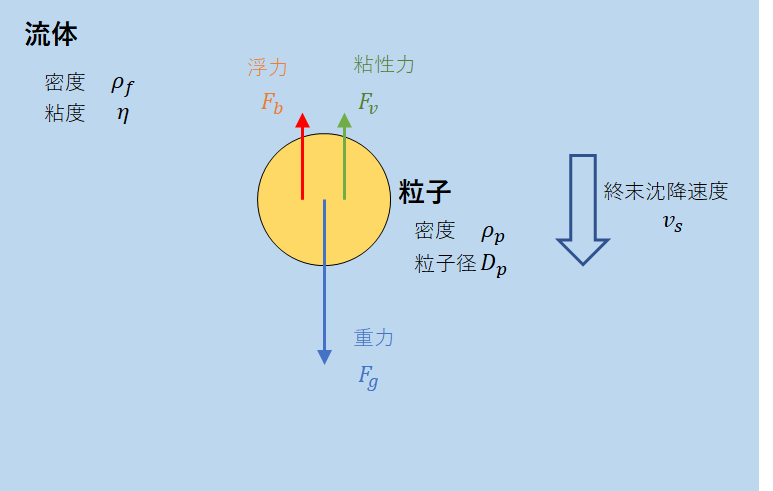
粒子が終末沈降速度v_sに達している時、等速直線運動となっているため、力のつり合いは以下のようになります。

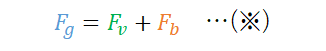
それぞれの力を具体的に式で表すと、

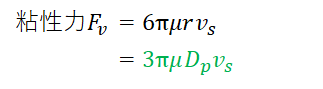
ここで、粘性力は流体の運動を記述するナビエ・ストークス方程式を解くことで得られる関係です。

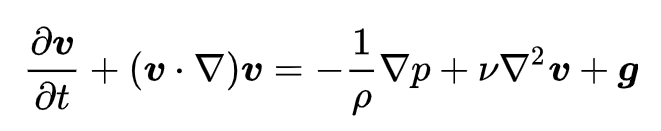
詳細の導出は難しく、割愛していますが(導出する気になりません)、

• 粘性力はナビエ・ストークス方程式から導出されていること
• 粘性力は速度v_sに比例すること

をわかっていただければOKかと思います。

さて、(※)にそれぞれ式を代入し、v_sについて解くと

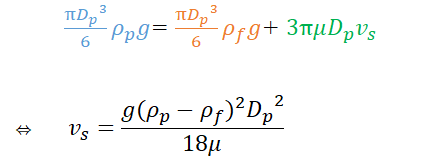
となり、ストークスの式が導出できました!

参考

1. 新・公害防止の技術と法規　汚水処理特論
2. Wikipedia “ストークスの式”
3. Wikipedia “ナビエ–ストークス方程式”